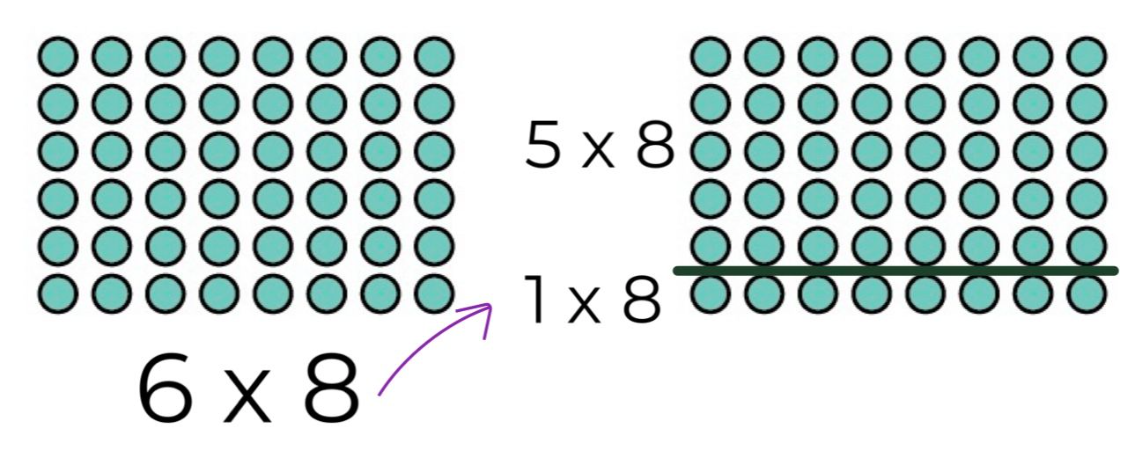What Is a Reasoning Strategy? Here Are Some Examples!
We've been talking about fact fluency, and in my previous post, I shared the three stages of developing fact fluency:
Counting Strategies
Reasoning Strategies
Fluency
Counting strategies are when children use the process of counting to figure out the answer. For example, an addition counting strategy for 5 + 4 would be for a child to say "5" and then count 4 more on their fingers: 6, 7, 8, 9. An example of a multiplication counting strategy for 4 x 6 would be for a child to skip count by 6s four times: 6, 12, 18, 24. In both of these examples, children are using a method of counting to figure out the answer.
After a child becomes comfortable using counting strategies, they're ready to progress to using a reasoning strategy. Repeated practice with reasoning strategies then progresses into fluency.
But what are reasoning strategies?
A reasoning strategy uses a child's understanding of number relationships and patterns (number sense) to figure out an unknown fact by relating it to one they already know.
In the rest of this post, I share examples of reasoning strategies for addition, subtraction, multiplication, and division. This is by no means a complete list, but instead is meant to help you visualize and better understand what a reasoning strategy includes.
Examples of Addition reasoning strategies:
One example of an addition reasoning strategy is to look for ways that an unknown addition fact is close to a fact your child already knows.
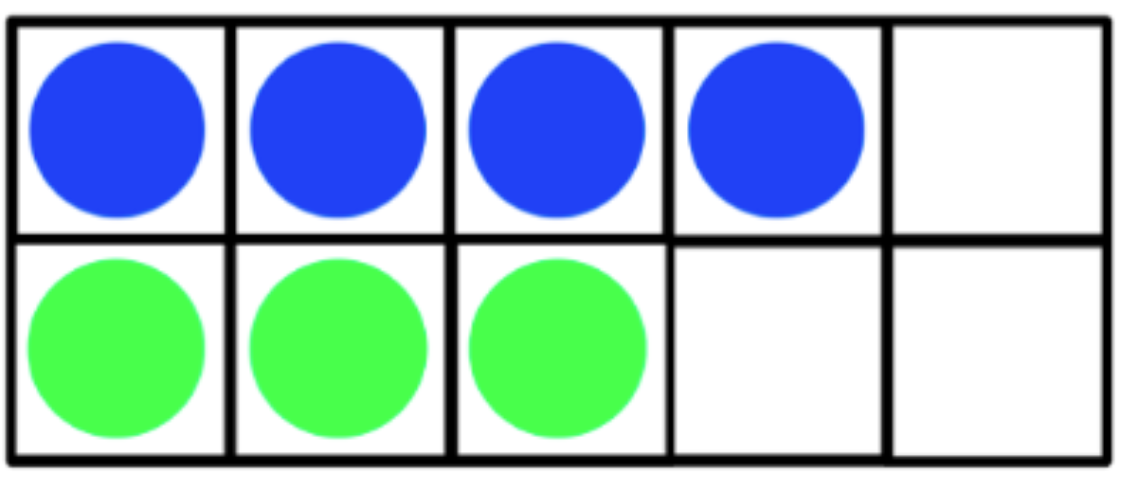
Maybe your child already knows that 3 + 3 = 6 because they've worked with that combination so many times. This can help them reason about a fact that is close to it, 4 + 3. You can show them a ten frame like the one below so they can visualize why 4 + 3 is really the same as 3 + 3 and one more. 3 + 3 = 6 and 4 + 3 is one more than 3 + 3 so 4 + 3 = 7.
Another example of an addition reasoning strategy is "making 10." In kindergarten, children build fluency with the combinations that make 10 and 10 is an easy number to add to because it has a 0 in the ones place. So a child who uses the make 10 strategy might reason about 7 + 8 by seeing that 8 needs 2 more to be 10, so it's really the same as 5 + 10, which is a much easier fact to figure out. Because 5 + 10 = 15 then 7 + 8 must also equal 15.
Examples of subtraction reasoning strategies:
In kindergarten, children learn about part-part-whole relationships. They build the understanding that two parts will always combine to make the same whole, and when either one of those parts is removed from the whole, the other part remains. For example, 4 and 3 will always combine to make 7, never a different number. When 4 is removed from 7, 3 remains. When 3 is removed from 7, 4 remains.
In first grade, this knowledge of part-part-whole relationships is extended to understanding the relationship between addition and subtraction. Children learn that subtraction can be written as an unknown addend problem, so 7 - 3 = ? is the same as ? + 3 = 7.
Using this understanding, a common subtraction reasoning strategy is to "think about addition." If I'm trying to figure out 7 - 3 = ?, I can ask myself, "What number plus 3 is the same as 7?"
Examples of multiplication reasoning strategies:
If your child has built fluency with addition and subtraction facts and is ready to move on to multiplication facts, you might be wondering where to start.
Just like with addition and subtraction, you'll want to start with counting strategies. For multiplication, this means using an array to make the connection between addition and multiplication.
For example, a child can look at this 5 by 4 array to see 5 groups of 4. They can solve this using repeated addition: 4 + 4 + 4 + 4 + 4 = ? which leads directly into understanding multiplication as combining repeated groups. 4 + 4 + 4 + 4 + 4 is the same as 5 groups of 4, which we can show as 5 x 4. Children often initially count by 4s five times to figure out the answer is 20.
This work with arrays leads nicely into the first multiplication reasoning strategy we'll discuss today: applying the commutative property.
The commutative property states that the order in which two numbers are added or multiplied doesn't change the answer. Children can use arrays to easily visualize why 5 x 4 and 4 x 5 lead to the same answer. 5 groups of 4 can be rotated to make 4 groups of 5, as shown in the arrays below.
So, using the commutative property, if a child doesn't already know the answer to 8 x 2 (8 groups of 2), they can visualize it as the same as 2 groups of 8, 2 x 8, and more quickly figure out that the answer is 16.
This is a common, and very helpful, reasoning strategy with the smaller 6, 7, 8 and 9 facts. A child who already knows their 2s and 3s facts, can now easily figure out 6 x 2, 6 x 3, 7 x 2, 7 x 3, and so on, simply by understanding that the order of a multiplication problem can be switched without changing the product (answer).
A second extremely helpful multiplication strategy that is made easier with arrays is what is often called the "break apart strategy." In this strategy, a child splits the array of an unknown fact into two arrays of known facts and then adds the products back together. For example, if a child doesn't know 6 x 8, but they do know their 5s and 1s facts, they could split 6 x 8 into (5 x 8) + (1 x 8) and add those two products (answers) together.
The array helps them understand why this works by making it easy to see that 6 groups of 8 is also the same as 5 groups of 8 plus 1 group of 8. 5 times 8 equals 40 and 1 times 8 equals 8, so 6 times 8 must be the same as 40 plus 8, 48.
This strategy later becomes the foundation for understanding the distributive property of multiplication.
Example of division reasoning strategies:
Similarly to the relationship between addition and subtraction facts, once a child builds fluency with multiplication facts, fluency with division facts becomes much easier. When a child understands multiplication as combining equal groups and division as splitting into equal groups, they can understand why 5 groups of 6 will always make 30, so 30 split into 5 groups must mean 6 in a group. Using this reasoning, they can think of division facts as finding an unknown factor. 30 ÷ 5 = ? is the same as ? x 5 = 30.