How to Make Math Make Sense
There's a popular math quote that says, "Children must hold math in their hands before they can hold it in their heads." The source of this quote is unknown, but it hits the nail on the head.
When I see a child struggling with mental or abstract math, the most common reason is that the child hasn't had enough time to make sense of the underlying mathematical concept with a hands-on tool before being asked to solve mentally or only with abstract symbols on paper.
In the research, this progression of understanding from a hands-on tool to mathematical symbols is called the Concrete-Representational-Abstract model and it explains a framework for helping children make sense of complex mathematical concepts.
And if there's a math concept your child is struggling to understand, this framework might be exactly what they need.
Often called CRA for short, the Concrete-Representational-Abstract model of teaching mathematics is based on the idea that mathematical symbols are used to represent mathematical concepts.
The symbols themselves are not the math. The symbols are a way to show the math.
For example, when we think of Algebra, we often think of equations. But the equations themselves are not the math concept. The equations are symbolic representations of the concept of equivalency and the process that can be used to determine an unknown value when we know two expressions are equal.
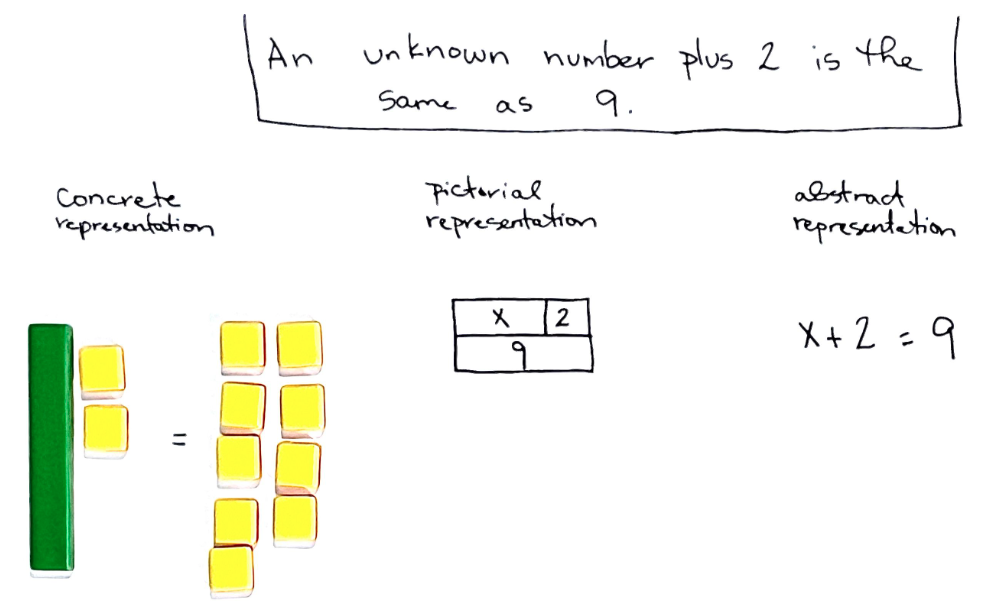
What do I mean? Look at these examples here. The algebra tiles, tape diagram, and equation all represent the same mathematical problem: an unknown number plus 2 is the same as 9. The symbolic equation, x + 2 = 9, isn't "the math." It's just the abstract representation of this math problem. The algebra tiles provide a concrete representation of the same math problem and the tape diagram is a pictorial representation of it.
This is important because so often math instruction jumps straight to the abstract representation: the version of any problem written out with just numbers and symbols. But this abstract representation can feel extremely vague to children, which makes sense, it is called "abstract" after all.
And this is where the CRA model comes in: When we illustrate math concepts with concrete and pictorial representations in addition to the abstract representations, we give the abstract representations meaning. Children are able to build a better understanding of the underlying mathematical concepts and connect that understanding to the abstract representations they see of those concepts.
Why is this helpful for parents? When our kids are struggling with a math concept, our first go-to is often to explain it the way we know how to do it. For most adults, this is the abstract representation. It works for us because we've built an understanding of it over the years. But it doesn't often click with our kids right away and this frequently leads to increased frustration for both parents and children.
When our children are struggling with an abstract or pictorial representation of a math concept, what they often need is to take it back to a concrete representation. The concrete representation allows them to experience the math in a way that the other representations don't, thus helping it become, well, more concrete. :)
I use this strategy with my own kids every time they struggle with a math problem. If you follow my Instagram stories, you know this happened recently with my 3rd grader who is learning about area and perimeter. He brought home perimeter work from school and had mixed up the calculations for area and perimeter on most of the problems. When I asked him to tell me the difference between the two he said, "I already know it now. Area is when you multiply and perimeter is when you add." He might as well have just said to me, "I don't really understand the difference, but I realized I mixed up the formulas." The formulas for area and perimeter of a rectangle are the abstract representations of these concepts, and when he couldn't explain what they meant, I knew we needed to go back to the concrete.
So I taped out a big 4 by 6 rectangle on our kitchen floor and we talked about what each measures. Area is the measurement of the space inside the rectangle, and he moved his hand across the space inside the giant rectangle. We counted up the squares inside the rectangle and discussed why this was the same as multiplying the length by the width.
Then we described perimeter as the distance around the outside of the shape, and he traced his finger along the outside border. We counted the length of the distance on each side and discussed why this was the same as adding up the units on each side of the rectangle. With repeated concrete representations like this, formulas like area = length x width and perimeter = 2(length + width) will make more sense to him.
So next time your child is struggling with a math concept, act it out. Try to think of a way you can use objects in your house to make the math concept concrete. (Google always has lots of good ideas too. Just search "concrete representation of [insert math concept]).